Supervised and unsupervised training with Hidden Markov Models
Hidden Markov Models in Supervised and unsupervised training
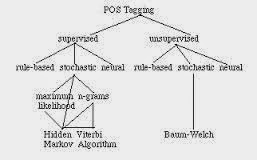
The probabilistic models used by Church and DeRose in the papers just cited were Hidden Markov Models (HMMs), imported from the speech recognition community. An HMM describes a probabilistic process or automaton that generates sequences of states and parallel sequences of output symbols. Commonly, a sequence of output symbols represents a sentence of English or of some other natural language. An HMM, or any model, that defines probabilities of word sequences (that is, sentences) of a natural language is known as a language model.
The probabilistic automaton defined by an HMM may be in some number of distinct states. The automaton begins by choosing a state at random. Then it chooses a symbol to emit, the choice being sensitive to the state. Next it chooses a new state, emits a symbol from that state, and the process repeats. Each choice is stochastic – that is, probabilistic. At each step, the automaton makes its choice at random from a distribution over output symbols or next states, as the case may be.
Which distribution it uses at any point is completely determined by the kind of choice, either emission of an output symbol or transition to a new state, and the identity of the current state. The actual model consists in a collection of numeric values, one for each possible transition or emission, representing the probability that the automaton chooses that particular transition or emission when making one of its stochastic choices. Learning an HMM is straightforward if one is provided with labeled data, meaning state sequences paired with output sequences. Each sequence pair is a record of the stochastic choices made by the automaton. To estimate the probability that the automaton will choose a particular value x when faced with a stochastic choice of type T , one can simply count how often the automaton actually chose x when making a choice of type T in the record of previous computations, that is, in the labeled data. If sufficient labeled data is available, the model can be estimated accurately in this way.
Church and DeRose applied HMMs to the problem of part-of-speech tagging by identifying the states of the automaton with parts of speech. The automaton generates a sequence of parts of speech, and emits a word for each part of speech. The result is a tagged text, which is a text in which each word is annotated with its part of speech. Supervised learning of an HMM for part-of-speech tagging is quite effective; HMM taggers for English generally have an error rate of 3.5 to 4 percent. Their effectiveness was what brought probabilistic models to the attention of computational linguists, as already mentioned.

Komentar
Posting Komentar